LeetCode Hot100笔记-下

Posted on Edited on In Views:
现在面试肯定有笔试环节，大部分的笔试题在 ht100 中又可以找到相似的思路。笔者在刷的时候对里面的知识点再次细化一下，感触颇深。本篇文章是下部分，包含另外的 50 道题。

简单

35. 搜索插入位置

image-20240607150135667

知识点：排序

使用 golang 中的 sort 包很容易解决，通过 sort.Find() 二分查找法的答案就是插入的位置。

1
2
3
4
5
6
func searchInsert(nums []int, target int) int {
    // return sort.SearchInts(nums, target)
    return sort.Search(len(nums), func(x int) bool {
        return nums[x] >= target
    })
}

20. 有效的括号

image-20240607154213837

知识点：栈

多种括号，最优方案就是使用栈，左括号就入栈，右括号就出栈匹配。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
func isValid(s string) bool {
    // 使用栈
    stack := make([]rune, 0)
    for _, v := range s {
        if v == ')' {
            if len(stack) > 0 && stack[len(stack)-1] == '(' {
                stack = stack[:len(stack)-1]
            } else {
                return false
            }
        } else if v == '}' {
            if len(stack) > 0 && stack[len(stack)-1] == '{' {
                stack = stack[:len(stack)-1]
            } else {
                return false
            }
        } else if v == ']' {
            if len(stack) > 0 &&  stack[len(stack)-1] == '[' {
                stack = stack[:len(stack)-1]
            } else {
                return false
            }
        } else {
            stack = append(stack, v)
        }
    }

    return len(stack) == 0 
}

121. 买卖股票的最佳时机

image-20240611170144958

知识点：动态规划，双指针

动态规划核心是定义状态以及状态转移方程，按照题目所说，状态可以定义为持有股票或者没有持有股票。

还有另外一个解法，就是使用双指针，一个指针向右移动，代表卖出的价格，左指针代表买入的价格，当出现更小值时移动左指针，取左右相差的最大值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func maxProfit(prices []int) (res int) {
    // dp 记录当前的两种状态，持有股票或者没有持有股票时的利润
    // 0 代表不持有，1代表持有
    dp := make([][2]int, len(prices))
    // 初始状态
    dp[0] = [2]int{0, 0 - prices[0]}
    
    for i := 1; i < len(prices); i++ {
        // 不持有，要么是将前一天的卖掉，要么是今天不购入，两者选最大值
        dp[i][0] = prices[i] + dp[i-1][1]
        dp[i][0] = max(dp[i][0], 0)
        res = max(res, dp[i][0])
        
        // 持有，要么是昨天就持有，要么是昨天不持有，今天持有，两者选最大值
        dp[i][1] = dp[i-1][1]
        dp[i][1] = max(dp[i][1], 0-prices[i])
    }
    //fmt.Println(dp)
    
    return res
}

70. 爬楼梯

image-20240612101256760

知识点：动态规划

使用动态规划是最好的方法，因为 dp[i] = dp[i-1] + dp[i-2] 是最容易想到的状态转移方程。

1
2
3
4
5
6
7
8
9
10
11
12
func climbStairs(n int) int {
    // dp 记录当前爬到楼梯的方法数
    dp := make([]int, n+1)
    dp[0], dp[1] = 1, 1
    
    for i := 2; i <= n; i++ {
        // 爬到 n 层，要么是 从 n-1 层爬上来，要么是从 n-2 层爬上来
        dp[i] = dp[i-1] + dp[i-2]
    }
    
    return dp[n]
}

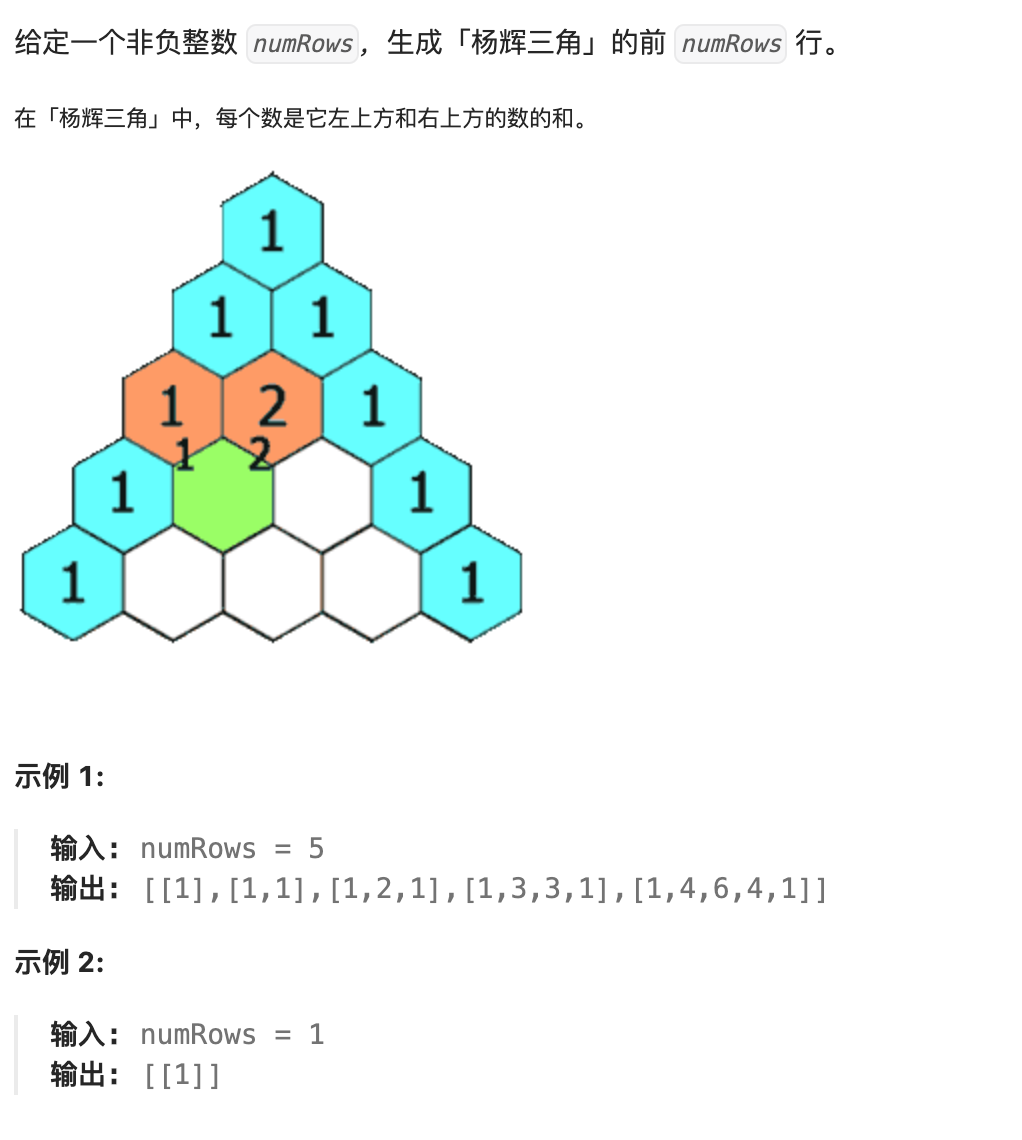
118. 杨辉三角

image-20240612101432830

知识点：模拟，数组

按照题目要求构建数组即可，按照要求可以知道 res[i][j] = res[i-1][j-1] + res[i-1][j] 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func generate(numRows int) [][]int {
    res := make([][]int, numRows)
    for i := 0; i < numRows; i++ {
        res[i] = make([]int, i+1)
        for j := 0; j < i+1; j++ {
            if j == 0 || j == i {
                res[i][j] = 1
            } else {
                res[i][j] = res[i-1][j-1] + res[i-1][j]
            }
        }
    }

    return res
}

136. 只出现一次的数字

image-20240612115103419

知识点：排序，hashmap

可以使用排序，然后便利一次，只要跟下一个数不相等，则说明是答案。

或者使用 hashmap，如果已经存在，则删除，如果没有，则插入，最后 hashmap 中剩下就是。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func singleNumber(nums []int) int {
    sort.Ints(nums)
    for i := 0;i < len (nums) ; {
        if i == len(nums)-1 || nums[i] != nums [i+1] {
                return nums[i]
        }
        j := i +1
        for nums[i] == nums[j] && j < len (nums) {
            j++ 
        }
        i = j
    }

    return 0
}

169. 多数元素

image-20240612115314364

知识点：排序，hashmap

可以先排序，然后中位数字就是，或者使用 hashmap 记录出现的次数，当大于一半时得到答案。

1
2
3
4
func majorityElement(nums []int) int {
    sort.Ints(nums)
    return nums[len(nums)>>1]
}

中等

200. 岛屿数量

image-20240607102430744

知识点：数组、bfs

可以将岛屿用 0 填充，判断填充的次数即可。填充时使用 bfs 往四个方向将 1 改成 0。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func numIslands(grid [][]byte) (res int) {
    m, n := len(grid), len(grid[0])
    var full func(x int, y int)
    dirs := [4][2]int{[2]int{-1, 0}, [2]int{0, 1}, [2]int{1, 0}, [2]int{0, -1}}
    full = func(x, y int) {
        grid[x][y] = 0
        // 四个方向
        for _, dir := range dirs {
            nx, ny := x+dir[0], y+dir[1]
            if nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == '1' {
                full(nx, ny)
            }
        }
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if grid[i][j] == '1' {
                full(i, j)
                res++
            }
        }
    }
    // fmt.Println(grid)

    return res
}

994. 腐烂的橘子

image-20240607103429993

知识点：数组、bfs

按照题目要求，可以使用 bfs 解决，将腐烂的橘子扩散出去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func orangesRotting(grid [][]int) (res int) {
    m, n := len(grid), len(grid[0])
    // 记录所有好的橘子个数,以及坏橘子的位置
    var total int
    bad := make([][2]int, 0, 10)
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            switch grid[i][j] {
            case 1:
                total++
            case 2:
                bad = append(bad, [2]int{i, j})
            }
        }
    }

    dirs := [4][2]int{[2]int{-1, 0}, [2]int{0, 1}, [2]int{1, 0}, [2]int{0, -1}}
    if len(bad) > 0 {
        res = -1
    }
    // 便利 bad 将四周的橘子腐烂
    for len(bad) > 0 {
        next := make([][2]int, 0, 10)
        for _, v := range bad {
            for _, dir := range dirs {
                nx, ny := v[0]+dir[0], v[1]+dir[1]
                if nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] == 1 {
                    next = append(next, [2]int{nx, ny})
                    grid[nx][ny] = 2
                    total--
                }
            }
        }
        res++
        bad = next
    }
    // fmt.Println(grid)

    if total != 0 {
        return -1
    }

    return res
}

207. 课程表

image-20240607111150989

知识点：数组、图、树

先将所有课程的关系做成一张图，然后判断某个学科是否没有前置即可学习，然后 bfs 扩散下去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
func canFinish(numCourses int, prerequisites [][]int) bool {
    // 记录学习了之后可以学习的课程
    total := make([][]int, numCourses)
    // 记录这么课程学习前需要学习什么课程
    need := make([][]int, numCourses)
    for _, v := range prerequisites {
        need[v[0]] = append(need[v[0]], v[1])
        total[v[1]] = append(total[v[1]], v[0])
    }

    // 获取没有前置的课程
    totalCourse := numCourses
    learned := make([]bool, numCourses)
    noNeed := make([]int, 0, numCourses)
    for i, v := range need {
        if len(v) == 0 {
            noNeed = append(noNeed, i)
            totalCourse--
            learned[i] = true
        }
    }

    for len(noNeed) > 0 {
        // 便利可以学习的课程
        next := make([]int, 0, numCourses)
        for _, v := range noNeed {
            // 判断后续可以学习的课程
            for _, i := range total[v] {
                if learned[i] {
                    continue
                }
                var flag bool
                // 判断这个课程所需要的是否都已经学习
                for _, j := range need[i] {
                    if !learned[j] {
                        flag = true
                        break
                    }
                }
                if !flag {
                    learned[i] = true
                    totalCourse--
                    next = append(next, i)
                }
            }
        }
        noNeed = next
    }
    // fmt.Println(learned)
    // fmt.Println(totalCourse)

    return totalCourse == 0
}

208. 实现 Trie (前缀树)

image-20240607112627891

知识点：前缀树

题目中已经明确表明由小写英文组成，是有限树，因此，可以使用数组代替 map 以提高性能。前缀树是一个嵌套结构，按照题目既要求判断是否有前缀，也判断是否有值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
type Trie struct {
    tree   [26]*Trie
    prefix bool
    value  bool
}

func Constructor() Trie {
    return Trie{}
}

func (this *Trie) Insert(word string) {
    for _, v := range word {
        if this.tree[v-'a'] == nil {
            this.tree[v-'a'] = &Trie{}
        }
        this = this.tree[v-'a']
        this.prefix = true
    }
    this.prefix = true
    this.value = true
}

func (this *Trie) Search(word string) bool {
    for _, v := range word {
        if this.tree[v-'a'] == nil {
            return false
        }
        this = this.tree[v-'a']
    }
    return this.value
}

func (this *Trie) StartsWith(prefix string) bool {
    for _, v := range prefix {
        if this.tree[v-'a'] == nil {
            return false
        }
        this = this.tree[v-'a']
    }
    return this.prefix
}

/**
 * Your Trie object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Insert(word);
 * param_2 := obj.Search(word);
 * param_3 := obj.StartsWith(prefix);
 */

46. 全排列

image-20240607113345025

知识点：数组，dfs，二进制

从题目可以判断，是需要返回所有的数字，并且乱序，可以使用 dfs 加上二进制记录已经选取的数字。

这里需要注意，二进制用于记录idx，而且是按照位来记录，避免使用数字记录造成影响。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func permute(nums []int) (res [][]int) {
    var dfs func(tmp []int, next int)
    dfs = func(tmp []int, next int) {
        if len(tmp) == len(nums) {
            t := make([]int, len(tmp))
            copy(t, tmp)
            res = append(res, t)
            return
        }

        for i, v := range nums {
            if next&(1<<i) != 1<<i {
                // 说明这个数字不存在
                tmp = append(tmp, v)
                dfs(tmp, next|(1<<i))
                // 回溯
                tmp = tmp[:len(tmp)-1]
            }
        }
    }
    dfs([]int{}, 0)

    return res
}

78. 子集

image-20240607114552837

知识点：二进制

需要返回子集，最好的方法就是使用二进制，如果是 0，则不返回，如果是 1 则返回。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func subsets(nums []int) (res [][]int) {
    total := 1 << len(nums)

    for i := 0; i < total; i++ {
        tmp := make([]int, 0, len(nums))
        for j := 0; j < len(nums); j++ {
            if i&(1<<j) == 1<<j {
                tmp = append(tmp, nums[j])
            }
        }
        res = append(res, tmp)
    }
    return res
}

17. 电话号码的字母组合

image-20240607114911345

知识点：枚举、递归、便利

三层便利，第一层是输入的数字，第二层是数字代表的字母，第三层是前面的 res，便利后相互组合，并且替代之前的 res

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func letterCombinations(digits string) (res []string) {
    if len(digits) == 0 {
        return nil
    }

    total := map[rune][]string{
        '2': []string{"a", "b", "c"},
        '3': []string{"d", "e", "f"},
        '4': []string{"g", "h", "i"},
        '5': []string{"j", "k", "l"},
        '6': []string{"m", "n", "o"},
        '7': []string{"p", "q", "r", "s"},
        '8': []string{"t", "u", "v"},
        '9': []string{"w", "x", "y", "z"},
    }
    
    res = []string{""}
    for _, digit := range digits {
        tmp := total[digit]
        newRes := make([]string, 0, len(res))
        for _, v := range res {
            for _, s := range tmp {
                newRes = append(newRes, v+s)
            }
        }
        res = newRes
    }
    
    return res
}

39. 组合总和

image-20240607115200694

知识点：递归

要寻找 target，其实也代表着寻找 target-num，递归下去，直到等于 0则是答案，小于 0 则返回。

为了加快速度，也可以先排序，如果小于 0，则不用往后面的递归下去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
func combinationSum(candidates []int, target int) (res [][]int) {
    // 使用 dfs 和回溯
    // 先排序，直到小于 0，则结束嵌套
    sort.Ints(candidates)
    var dfs func(start int, next int, tmp []int)
    dfs = func(start int, next int, tmp []int) {
        // 结束条件
        if next == 0 {
            // 这里要拷贝一份，避免回溯后出现变更
            tmpRes := make([]int, len(tmp))
            copy(tmpRes, tmp)
            res = append(res, tmpRes)
            return
        }
        if next < 0 {
            return
        }
        // 开始计算和回溯
        for i := start; i < len(candidates); i++ {
            if next < candidates[i] {
                return
            }
            tmp = append(tmp, candidates[i])
            dfs(i, next-candidates[i], tmp)
            // 回溯
            tmp = tmp[:len(tmp)-1]
        }
    }
    dfs(0, target, []int{})

    return res
}

22. 括号生成

image-20240607115614324

知识点：dfs，枚举

使用 dfs 枚举，放括号和反括号，记录括号和反括号的数量，如果反括号大于 0，说明不合法，枚举的时候跳过不合法的组合。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
func generateParenthesis(n int) (res []string) {
    var dfs func(str string, left int)
    dfs = func(str string, left int) {
        if left == 0 {
            if check(str) {
                res = append(res, str)
            }
            return
        }

        dfs(str+"(", left-1)
        dfs(str+")", left-1)
    }
    dfs("", 2*n)
    return
}

func check(str string) bool {
    var tmp int
    for _, v := range str {
        if v == '(' {
            tmp++
        } else {
            tmp--
        }
        if tmp < 0 {
            return false
        }
    }
    return tmp == 0
}

79. 单词搜索

image-20240607143423633

知识点：bfs

便利数组，找到开头的，然后使用 dfs 便利下去，直到将所有的都找到，避免往回走，还需要使用回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
func exist(board [][]byte, word string) bool {
    // dfs 回溯,如果找到择继续往下找，如果没有找到，则回溯
    m, n := len(board), len(board[0])
    directions := [4][2]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
    
    var dfs func(i, j int, target string) bool
    dfs = func(i, j int, target string) bool {
        //fmt.Println(i, j, target)
        // 上下左右找
        if target == "" {
            return true
        }
        
        for _, direction := range directions {
            tmpI := i + direction[0]
            tmpJ := j + direction[1]
            if tmpI >= 0 && tmpI < m &&
                tmpJ >= 0 && tmpJ < n &&
                board[tmpI][tmpJ] == target[0] {
                board[tmpI][tmpJ] = '0'
                res := dfs(tmpI, tmpJ, target[1:])
                // 回溯
                board[tmpI][tmpJ] = target[0]
                if res {
                    return res
                }
            }
        }
        
        return false
    }
    
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if board[i][j] == word[0] {
                board[i][j] = '0'
                res := dfs(i, j, word[1:])
                if res {
                    return res
                }
                board[i][j] = word[0]
            }
        }
    }
    
    return false
}

131. 分割回文串

image-20240607143622901

知识点：动态规划，dfs，回溯

这个题目放在中等里面我还以为有更加简单的方法，但是实际上依然是使用 dp ，记录从 i 到 j 是否是一个回文，所有的子串都确定下来之后，再使用 dfs 将结果构造出来，而且由于有多种情况，还需要使用回溯。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
func partition(s string) (res [][]string) {
    n := len(s)
    dp := make([][]bool, n)
    for i := 0; i < n; i++ {
        dp[i] = make([]bool, n)
        dp[i][i] = true
    }

    for i := n-1; i >= 0; i-- {
        for j := i + 1; j < n; j++ {
            dp[i][j] = s[i] == s[j]
            if i+1 <= j-1 {
                dp[i][j] = dp[i][j] && dp[i+1][j-1]
            }
        }
    }
    // fmt.Println(dp)

    var dfs func(last []string, idx int)
    dfs = func(last []string, idx int) {
        if idx == n {
            tmp := make([]string, len(last))
            copy(tmp, last)
            res = append(res, tmp)
            return
        }

        for i := idx; i < n; i++ {
            if dp[idx][i] {
                last = append(last, s[idx:i+1])
                dfs(last, i+1)
                last = last[:len(last)-1]
            }
        }
    }

    for i := 0; i < n; i++ {
        if dp[0][i] {
            dfs([]string{s[:i+1]}, i+1)
        }
    }

    return res
}

74. 搜索二维矩阵

image-20240607151013483

知识点：排序检索

两个方法，方法 1 ，每一行二分法

方法 2，右上角往左下角移动，小于则左移，大于则下移动

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func searchMatrix(matrix [][]int, target int) bool {
    // 方法 1 ，每一行二分法
    // 方法 2，右上角往左下角移动，小于则左移，大于则下移动
    m, n := len(matrix), len(matrix[0])
    i, j := 0, n-1
    for i < m && j >= 0 {
        if matrix[i][j] > target {
            j--
        } else if matrix[i][j] < target {
            i++
        } else {
            return true
        }
    }
    
    return false
}

34. 在排序数组中查找元素的第一个和最后一个位置

image-20240607151101915

知识点：排序检索

从题目中很容易判断要使用二分查找法，找到当前插入的则是查询 target，找到结束的，则是 target+1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
func searchRange(nums []int, target int) []int {
    // 二分法，查询当前数字和+1的数字
    idx := sort.Search(len(nums), func(i int) bool {
        return nums[i] >= target
    })
    if idx < len(nums) && nums[idx] == target {
        end := sort.Search(len(nums), func(i int) bool {
            return nums[i] >= target+1
        })
        return []int{idx, end - 1}
    }
    
    return []int{-1, -1}
}

33. 搜索旋转排序数组

image-20240607151256139

知识点：数组，二分法

核心逻辑也是使用二分法，只是二分法的变种，也就是分情况讨论。分四种情况讨论：

  1. 中值落点在前半部分，target 大于中值，此时移动左边，将右边继续处理
  2. 中值落点在前半部分，target 小于中值，此时移动右边，左边是一个标准的二分法，将左边继续处理
  3. 中值落点在后半部分，target 大于中值，此时移动左边，右边是一个标准的二分法，将右边继续处理
  4. 中值落点在后半部分，target 小于中值，此时移动右边，将左边继续处理

面试的时候容易分不清，因此建议先写思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func search(nums []int, target int) int {
    // 使用二分法
    // 循环条件是 左边小于右边，避免相同的时候无法退出循环
    // 判断条件是 < target，则移动左边，
    // 左边移动的时候直接到 mid，右边移动的时候 -1
    
    l, r := 0, len(nums)
    for l < r {
        mid := (l + r) >> 1
        //fmt.Println(l, r, nums[mid])
        
        // 不好判断是不存在，还是存在右边，因此要手动判断是否相同
        if nums[mid] == target {
            return mid
        }
        
        if nums[mid] >= nums[0] {
            if target >= nums[0] && target < nums[mid] {
                r = mid - 1
            } else {
                l = mid + 1
            }
        } else {
            if target < nums[0] && target > nums[mid] {
                l = mid + 1
            } else {
                r = mid - 1
            }
        }
    }
    
    if r < len(nums) && nums[r] == target {
        return r
    }
    
    return -1
}

153. 寻找旋转排序数组中的最小值

image-20240607151933072

知识点：二分法，数组排序查询

看到题目就很容易想到使用二分法，如果中值大于 nums[0] 说明要移动左边，如果小于或等于 nums[0] 说明要移动右边，为了避免跳过，移动左边+1，移动右边直接赋予；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func findMin(nums []int) int {
    l, r := 0, len(nums)
    for l < r {
        mid := (l + r) >> 1
        if nums[mid] >= nums[0] {
            if nums[mid] > nums[len(nums)-1] {
                l = mid + 1
            } else {
                r = mid
            }
        } else {
            r = mid
        }
    }
    
    return nums[l]
}

155. 最小栈

image-20240607160745964

知识点：栈、最小值

这里不仅仅需要一个栈，还需要获取当前的最小值。如果使用排序，容易出现超时，因此可以使用取巧的方法，就是记录入栈时，同步记录一个当前的最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// 使用数组作为栈
// 使用第二个数组存储当数据存入时的最小值
type MinStack struct {
    nums []int
    less []int 
}

func Constructor() MinStack {
    return MinStack{
        nums: make([]int, 0),
        less: make([]int, 0),
    }
}

func (this *MinStack) Push(val int) {
    this.nums = append(this.nums, val)
    if len(this.less) == 0 || val < this.less[len(this.less)-1]{
        this.less = append(this.less,val)
    } else {
        this.less = append(this.less,this.less[len(this.less)-1])
    }
}

func (this *MinStack) Pop() {
    this.nums = this.nums[:len(this.nums)-1]
    this.less = this.less[:len(this.less)-1]
}

func (this *MinStack) Top() int {
    return this.nums[len(this.nums)-1]
}

func (this *MinStack) GetMin() int {
    return this.less[len(this.less)-1]
}

/**
 * Your MinStack object will be instantiated and called as such:
 * obj := Constructor();
 * obj.Push(val);
 * obj.Pop();
 * param_3 := obj.Top();
 * param_4 := obj.GetMin();
 */

394. 字符串解码

image-20240607160908574

知识点：递归，字符串，栈

通过题目可以判断使用递归是最好的选择，当出现括号时，将括号内的内容进行递归处理，将返回的结果使用数字个数复制。

记录括号的方式是使用栈，出栈的时候代表是一个子串，进行递归。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func decodeString(s string) string {
    // 使用栈，左括号入栈，右括号出栈，出栈后判断栈内字符串
    // 递归使用数字 + 单个栈的数据
    stack := make([]int, 0)
    stackN := make([]int, 0)
    tmpN := ""
    
    tmpRes := ""
    for i, v := range s {
        if v == '[' {
            stack = append(stack, i)
            n, _ := strconv.Atoi(tmpN)
            tmpN = ""
            stackN = append(stackN, n)
        } else if v == ']' {
            // 出栈
            tmp := stack[len(stack)-1]
            stack = stack[:len(stack)-1]
            // 递归的结果
            tmpS := decodeString(s[tmp+1 : i]) 
            // 复制
            tmpN := stackN[len(stackN)-1]
            stackN = stackN[:len(stackN)-1]
            
            tmpS = strings.Repeat(tmpS, tmpN-1)
            tmpRes += tmpS
        } else if v >= 'a' && v <= 'z' {
            tmpRes += string(v)
        } else {
            tmpN += string(v)
        }
    }
    
    return tmpRes
}

739. 每日温度

image-20240607161135053

知识点：栈

使用递减栈记录索引，出栈的时候表示出栈的那天有最高温

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func dailyTemperatures(temperatures []int) []int {
    // 单调递减栈，出来的时候代表今天是更高温
    stack := make([]int, 0, len(temperatures))
    res := make([]int, len(temperatures))
    for i, v := range temperatures {
        for len(stack) > 0 && v > temperatures[stack[len(stack)-1]] {
            tmp := stack[len(stack)-1]
            stack = stack[:len(stack)-1]
            res[tmp] = i - tmp
        }
        stack = append(stack, i)
    }
    // 最后出栈的都是 0
    return res
}

215. 数组中的第K个最大元素

image-20240607165700329

知识点：栈

使用栈，记录前 k 个最大的元素，当栈满的时候就出栈，最后的结果就是栈顶元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
func findKthLargest(nums []int, k int) int {
    // 使用堆，存储最小堆，返回最小值，也就是第 k 个值，可以保证 heap[0] 是第 k 大的值
    stackH := &h{}
    
    for _, num := range nums {
        heap.Push(stackH, num)
        for len(*stackH) > k {
            heap.Pop(stackH)
        }
    }
    
    return (*stackH)[0]
}

type h []int

func (h *h) Len() int {
    return len(*h)
}

func (h *h) Swap(i, j int) {
    (*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}

func (h *h) Less(i, j int) bool {
    return (*h)[i] < (*h)[j]
}

func (h *h) Push(x interface{}) {
    *h = append(*h, x.(int))
}

func (h *h) Pop() interface{} {
    x := (*h)[len(*h)-1]
    *h = (*h)[:len(*h)-1]
    return x
}

347. 前 K 个高频元素

image-20240607170628131

知识点：堆

简单方法是使用 hashmap，然后取出来排序。

但是应该使用堆更好一些，先使用对应长度的数组，记录对应 idx 出现的次数，然后使用k 个大堆，将数据放进去，满员的时候出堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func topKFrequent(nums []int, k int) []int {
    // hashmap 记录出现的数字和次数
    // 拿出来排序
    total := make(map[int]int)
    for _, num := range nums {
        total[num]++
    }
    tmp := make([][]int, 0, len(total))
    
    for k, v := range total {
        tmp = append(tmp, []int{k, v})
    }
    sort.Slice(tmp, func(i, j int) bool {
        return tmp[i][1] > tmp[j][1]
    })
    
    res := make([]int, 0, k)
    for i := 0; i < k; i++ {
        res = append(res, tmp[i][0])
    }
    
    return res
}

55. 跳跃游戏

image-20240611172113131

知识点：动态规划，双指针

可以使用动态规划，代表 idx 的位置是否可以跳到，状态转移等于前面可以跳到的点，是否可达当前点；

也可以使用双指针，左边指针遍历可达的点，右边指针往右边移动，移动到最大可达的点。

1
2
3
4
5
6
7
8
9
10
func canJump(nums []int) bool {
    // 双指针
    l, r := 0, 0
    // 移动左指针的时候，移动右边指针
    for ; l <= r && l < len(nums); l++ {
        r = max(r, l+nums[l])
    }
    
    return  l >= len(nums)
}

45. 跳跃游戏 II

image-20240611172748307

知识点：动态规划

使用动态规划，记录跳到当前点的最小跳跃数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func jump(nums []int) int {
    // 这种情况就只能使用 dp
    // dp 代表到达某处的最小次数
    dp := make([]int, len(nums))
    dp[0] = 0
    for i := 1; i < len(nums); i++ {
        dp[i] = math.MaxInt
        for j := i - 1; j >= 0; j-- {
            // 判断是否可以通过点 j 跳到当前节点
            if j+nums[j] >= i {
                dp[i] = min(dp[i], dp[j]+1)
            }
        }
    }
    
    return dp[len(dp)-1]
}

763. 划分字母区间

image-20240611172938787

知识点：动态规划，双指针、贪心

这是一个很明显的局部性问题，可以使用动态规划来解决，dp 记录长度到 idx 时的长度列表，以及一个数组记录最开始出现的位置，当出现重复的时候，便利前一个的长度列表，直到可以放下当前位置。

但是在编码的时候可以感觉到计算比较复杂，因此可以改用更加简便的方法，也就是使用双指针和贪心。

使用双指针的时候需要确定左指针和右指针要代表什么，按照题目要求，肯定是代表子串的起止位置，在移动的时候为了确定左边界和右边界，则需要先便利一次，记录所有字符出现的最后的位置，作为右指针的移动逻辑判断。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func partitionLabels(s string) (res []int) {
    // 记录最后出现的位置
    last := [26]int{}
    for i, v := range s {
        last[v-'a'] = i
    }

    // 双指针，贪心
    var l, r int
    for i := 0; i < len(s); i++ {
        r = max(r, last[s[i]-'a'])
        if i == r {
            res = append(res, r-l+1)
            l = r + 1
        }
    }

    return res 
}

198. 打家劫舍

image-20240612101907741

知识点：动态规划

局部问题的解法，一般都会想到使用动态规划，记录当前房屋偷窃或者不偷窃的金额，最终答案即使最后一间屋子偷窃或者不偷窃的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func rob(nums []int) int {
    // dp，代表这家偷和不偷的时候的最高金额
    dp := make([][2]int, len(nums))
    // 0 代表这家不偷，1代表这家偷
    dp[0] = [2]int{0, nums[0]}
    
    for i := 1; i < len(nums); i++ {
        // 这一家不偷，取上一家没偷或者偷了的最大值
        dp[i][0] = max(dp[i-1][0], dp[i-1][1])
        // 这一家偷，就只能是上一家不偷
        dp[i][1] = dp[i-1][0] + nums[i]
    }
    
    return max(dp[len(dp)-1][0], dp[len(dp)-1][1])
}

279. 完全平方数

image-20240612102046542

知识点：动态规划

使用动态规划，记录数字的平方数最少数量，dp[i] = min(dp[i-x*x] + 1) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
func numSquares(n int) int {
    // 动态规划，
    // n 为 1...m 的 dp[j] + 1 的 min
    dp := make([]int, n+1)
    dp[1] = 1

    for i := 2; i <= n; i++ {
        dp[i] = dp[i-1] + 1
        for j := 2; i-j*j >= 0; j++ {
            dp[i] = min(dp[i], dp[i-j*j]+1)
        }
    }
    //fmt.Println(dp)
    return dp[n]
}

322. 零钱兑换

image-20240612102654337

知识点：动态规划

碰到这个问题，首先可能会想到使用贪心，先拿取大额硬币，但是如果出现 4,5 这样，需要组合成 8，则可能还需要回溯，此时问题就复杂了。因此可以转换一下思路，使用动态规划，记录从 0 到 amount 的硬币个数。状态转移方程是 dp[i] = min(dp[i], dp[i-coin]+1) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
func coinChange(coins []int, amount int) int {
    // 代表金额为 i 时的组合数
    dp := make([]int, amount+1)
    // 初始状态
    dp[0] = 0
    
    for i := 1; i <= amount; i++ {
        // 状态转移方程，为减去 coin 的最小次数
        dp[i] = math.MaxInt
        for _, coin := range coins {
            if i-coin >= 0 && dp[i-coin] != -1 {
                dp[i] = min(dp[i], dp[i-coin]+1)
            }
        }
        if dp[i] == math.MaxInt {
            dp[i] = -1
        }
    }
    //fmt.Println(dp)
    
    return dp[amount]
}

139. 单词拆分

image-20240612103351407

知识点：动态规划

使用动态规划，记录到 idx 的子串是否可以组成，状态转移方程为 dp[i] = dp[i-j]&&s[i-j:i]，其中 s[i-j:i] 在字典中

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func wordBreak(s string, wordDict []string) bool {
    // 使用字典树
    // 或者使用动态规划
    total := make(map[string]bool)
    for _, word := range wordDict {
        total[word] = true
    }
    // dp 代表到达字符串 s 是否可以组合
    dp := make([]bool, len(s)+1)
    // 初始化，空的可以
    dp[0] = true
    for i := 0; i <= len(s); i++ {
        // 查找前面的 dp，看是有有存在的，然后判断从 j-i 之间是否存在
        for j := 0; j <= i; j++ {
            if dp[j] && total[s[j:i]] {
                dp[i] = true
                break
            }
        }
    }
    
    //fmt.Println(dp)
    return dp[len(s)]
}

300. 最长递增子序列

image-20240612103808758

知识点：动态规划

使用动态规划，记录当结尾为 i 时的最长子序列，可以直到状态转移方程是 dp[i] = max(dp[i], dp[j]+1)，j<i&&nums[j]<nums[i]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func lengthOfLIS(nums []int) (res int) {
    // 动态规划
    // 代表当结尾为 i 时的最长子序列
    dp := make([]int, len(nums))
    dp[0] = 1
    res = 1

    for i := 1; i < len(nums); i++ {
        dp[i] = 1
        // 往前面找小于自己的数
        for j := i - 1; j >= 0; j-- {
            if nums[j] < nums[i] {
                dp[i] = max(dp[i], dp[j]+1)
            }
        }
        res = max(res, dp[i])
    }
    // fmt.Println(dp)

    return res
}

152. 乘积最大子数组

image-20240612104557479

知识点：动态规划

使用 dp，记录当 i 是子数组的结尾时的最大非负乘积和最小负乘积。状态转移方程则是判断前一个 dp 和自己的乘积，如果等于 0，则判断是否放弃，如果小于 0，则记录最大负，如果大于 0，则记录最大非负。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func maxProduct(nums []int) (res int) {
    // 动态规划
    // 记录当 i 为子数组末尾时的最大乘积
    // 0 代表正最大值，1代表负最大值
    dp := make([][2]int, len(nums))
    if nums[0] > 0 {
        dp[0][0] = nums[0]
    } else if nums[0] < 0 {
        dp[0][1] = nums[0]
    }
    res = nums[0]
    
    // 状态转移是如果小于 0，则获取前面的是否小于 0，如果是，则乘以，得到一个大于 0，然后在这再看前面的
    // 如果大于 0，跟前面的相乘
    for i := 1; i < len(nums); i++ {
        if nums[i] > 0 {
            // 不带前面的
            dp[i][0] = nums[i]
            
            // 带上前面的
            dp[i][0] = max(nums[i], dp[i-1][0]*nums[i])
            // 小于 0
            dp[i][1] = dp[i-1][1] * nums[i]
        } else if nums[i] < 0 {
            dp[i][0] = dp[i-1][1] * nums[i]
            
            // 小于 0
            dp[i][1] = nums[i]
            dp[i][1] = min(dp[i][1], dp[i-1][0]*nums[i])
        }
        res = max(res, dp[i][0])
    }
    //fmt.Println(dp)
    return res
}

416. 分割等和子集

image-20240612105142632

知识点：动态规划

先获取总和，然后判断总和是否可以被 2 整数以及获取最大数，不可以或者最大数超过半数的话说明可以直接判断无法相等。然后使用 dp，便利数组，便利 dp，需要注意顺序，避免重复硬币造成影响，相当于硬币一个一个往里面加，而且便利 dp 的时候要从后往前便利，也避免重复添加相同的硬币造成影响，dp[i] = dp[i-j]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func canPartition(nums []int) bool {
    // 转换成选择 nums 中的数字组成 x
    var total, m int
    for _, num := range nums {
        total += num
        if num > m {
            m = num
        }
    }
    if total%2 != 0 {
        return false
    }
    x := total / 2
    if m > x {
        return false
    } else if m == x {
        return true
    }

    // 表示当选取 i 个数字时，是否可以组合成 x
    dp := make([]bool, x+1)
    dp[0] = true

    for j := 0; j < len(nums); j++ {
        for i := len(dp) - 1; i >= 0; i-- {
            if i-nums[j] >= 0 && dp[i-nums[j]] {
                dp[i] = true
            }
        }
    }

    // fmt.Println(dp)

    return dp[x]
}

62. 不同路径

image-20240612111854751

知识点：动态规划

机器人移动的问题都可以使用动态规划来解决，dp[i][j] = dp[i][j-1] + dp[i-1][j]，需要注意的是要在上面和左边包一层，为了更好的计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func uniquePaths(m int, n int) int {
    // 使用 dp，在左边和上面包一层
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }
    dp[1][1] = 1
    
    for i := 1; i <= m; i++ {
        for j := 1; j <= n; j++ {
            if !(i == 1 && j == 1) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
            }
        }
    }
    //fmt.Println(dp)
    
    return dp[m][n]
}

64. 最小路径和

image-20240612112106776

知识点：动态规划

跟机器人移动一样，差别是比较向下或者向右移动的最小步数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func minPathSum(grid [][]int) int {
    // dp 同样的包一层
    m, n := len(grid), len(grid[0])
    dp := make([][]int, m+1)
    for i := range dp {
        dp[i] = make([]int, n+1)
        dp[i][0] = math.MaxInt
        if i == 0 {
            for j := 0; j <= n; j++ {
                dp[i][j] = math.MaxInt
            }
        }
    }
    dp[1][1] = grid[0][0]
    
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if !(i+1 == 1 && j+1 == 1) {
                dp[i+1][j+1] = grid[i][j] + min(dp[i][j+1], dp[i+1][j])
            }
        }
    }
    
    //fmt.Println(dp)
    
    return dp[m][n]
}

5. 最长回文子串

image-20240612112227196

知识点：动态规划

也是一个局部到全局的问题，使用动态规划，记录 i 到 j 这个子串是否是回文子串，然后从左向右移动 j，从右向左移动i 判断回文，记录最长答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
func longestPalindrome(s string) (res string) {
    m := len(s)
    dp := make([][]bool, m)
    for i := 0; i < m; i++ {
        dp[i] = make([]bool, m)
        dp[i][i] = true
    }
    res = s[0:1]

    // 状态转移
    for j := 1; j < m; j++ {
        for i := j - 1; i >= 0; i-- {
            if s[i] == s[j] && (i == j-1 || dp[i+1][j-1]) {
                dp[i][j] = true 

                if j - i + 1 > len(res) {
                    res = s[i:j+1]
                }
            }
        }
    }

    return res 
}

1143. 最长公共子序列

image-20240612112946636

知识点：动态规划

使用动态规划，dp[i][j] 代表 text1 长度为 i，text2 长度为 j 时，最长公共子序列的长度。这个题目没有别的方法，只能记住要使用动态规划，自己想比较难想到。状态转移方程则是 if text1[i] == text2[j];dp[i][j] = dp[i-1][j-1]+1; else max(dp[i-1][j],dp[i][j-1])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func longestCommonSubsequence(text1 string, text2 string) (res int) {
    m, n := len(text1), len(text2)
    dp := make([][]int, m+1)
    for i := 0; i < m+1; i++ {
        dp[i] = make([]int, n+1)
    }
    dp[0][0] = 0

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            // 状态转移方程
            if text1[i] == text2[j] {
                dp[i+1][j+1] = dp[i][j] + 1
            } else {
                dp[i+1][j+1] = max(dp[i][j+1], dp[i+1][j])
            }
            res = max(res,dp[i+1][j+1])
        }
    }
    // fmt.Println(dp)

    return res 
}

72. 编辑距离

image-20240612113630009

知识点：动态规划

跟上面最长公共子序列一样，都是直接使用动态规划，平时想不出来的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func minDistance(word1 string, word2 string) int {
    m, n := len(word1), len(word2)
    dp := make([][]int, m+1)
    for i := 0; i < m+1; i++ {
        dp[i] = make([]int, n+1)
        if i == 0 {
            for j := 0; j < n+1; j++ {
                dp[i][j] = j
            }
        }
        dp[i][0] = i
    }

    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            // 状态转移方程
            if word1[i] == word2[j] {
                dp[i+1][j+1] = dp[i][j]
            } else {
                dp[i+1][j+1] = min(min(dp[i][j], dp[i+1][j]), dp[i][j+1]) + 1
            }
        }
    }
    // fmt.Println(dp)

    return dp[m][n]
}

75. 颜色分类

image-20240612115424887

知识点：排序

虽然通过排序函数可以直接实现，但是既然题目要求不能使用，那么可以使用三指针，类似冒泡排序的方式，从左往右便利，左边指针往右，右边指针往左，如果便利到 0，则跟左指针调换，如果便利到 1 则跳过，如果便利到 2 则跟右边指针调换。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func sortColors(nums []int) {
    l, r := 0, len(nums)-1
    for i := 0; i <= r; i++ {
        switch nums[i] {
        case 0:
            nums[l], nums[i] = nums[i], nums[l]
            l++
        case 1:

        case 2:
            nums[r], nums[i] = nums[i], nums[r]
            r--
            i--
        }
        // fmt.Println(nums)
    }
}

31. 下一个排列

image-20240612140905238

知识点：模拟

这个题目没有什么逻辑，面试时如果碰到，只能死记硬背，先找到非降序的值，然后再找到第一个比这个值更大的值，两个值交换，再将非降序值后面反转一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func nextPermutation(nums []int) {
    // 找到非降序的值
    i, j := len(nums)-2, len(nums)-1
    for ; i >= 0; i-- {
        if nums[i] < nums[i+1] {
            break
        }
    }
    if i >= 0 {
        for ; j > i; j-- {
            if nums[j] > nums[i] {
                break
            }
        }
        // 交换 i，j
        nums[i], nums[j] = nums[j], nums[i]
    }

    // 反转 i 后面的位置
    for k := 1; k <= (len(nums)-i)>>1; k++ {
        nums[i+k], nums[len(nums)-k] = nums[len(nums)-k], nums[i+k]
    }
}

287. 寻找重复数

image-20240612151521079

知识点：模拟

这个题目也不明白为什么会被放在中等，使用一个临时数据记录出现过的数字即可。

1
2
3
4
5
6
7
8
9
10
func findDuplicate(nums []int) int {
    tmp := make([]bool,len(nums)+1)
    for _,v := range nums {
        if tmp[v] {
            return v 
        }
        tmp[v] = true 
    }
    return -1
}

困难

51. N 皇后

image-20240607145855183

知识点：dfs、回溯

通过题目很明显的可以知道要使用 dfs 和回溯，确定一个点之后，使用 dfs，从下一行开始便利，如果不满足条件，则返回，返回后回溯掉前面下的点。

面试的时候写这种题目核心在于不紧张理清楚思路，思路清晰后题目就会很简单，因此推荐在解题的时候先些注释的逻辑。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
func solveNQueens(n int) (res [][]string) {
    total = n
    
    // 使用回溯的方法
    var dfs func(grid [][]byte, last int)
    dfs = func(grid [][]byte, last int) {
        // 结束，找到了这个
        if last == 0 {
            fmt.Println(grid)
            tmp := make([]string, 0, n)
            for i := 0; i < n; i++ {
                tmp = append(tmp, string(grid[i]))
            }
            res = append(res, tmp)
            return
        }
        
        // 开始找寻下一个地方
        i := n - last
        for j := 0; j < n; j++ {
            if check(i, j, grid) {
                // 通过，这个点可以
                grid[i][j] = 'Q'
                // 去计算下一个
                dfs(grid, last-1)
                // 回溯
                grid[i][j] = '.'
            }
        }
    }
    
    grid := make([][]byte, n)
    for i := 0; i < n; i++ {
        grid[i] = make([]byte, n)
        for j := 0; j < n; j++ {
            grid[i][j] = '.'
        }
    }
    
    dfs(grid, n)
    
    return res
}

var total int

// 检查 i,j 是否满足
func check(i int, j int, grid [][]byte) bool {
    // 同一行，同一列
    for x := 0; x < total; x++ {
        if grid[i][x] == 'Q' {
            return false
        }
        if grid[x][j] == 'Q' {
            return false
        }
    }
    
    // x 轴和 y 轴
    x, y := i, j
    for x >= 0 && x < total &&
        y >= 0 && y < total {
        if grid[x][y] == 'Q' {
            return false
        }
        x += 1
        y += 1
    }
    x, y = i, j
    for x >= 0 && x < total &&
        y >= 0 && y < total {
        if grid[x][y] == 'Q' {
            return false
        }
        x -= 1
        y -= 1
    }
    x, y = i, j
    for x >= 0 && x < total &&
        y >= 0 && y < total {
        if grid[x][y] == 'Q' {
            return false
        }
        x += 1
        y -= 1
    }
    x, y = i, j
    for x >= 0 && x < total &&
        y >= 0 && y < total {
        if grid[x][y] == 'Q' {
            return false
        }
        x -= 1
        y += 1
    }
    
    return true
}

4. 寻找两个正序数组的中位数

image-20240607152427213

知识点：堆，排序

方法有两个，一个比较简单，就是合并，然后排序，然后取中值；

第二个比较有含量，使用两个堆，一个大堆一个小堆，大堆存储小值，小堆存储大值，先放到小堆里面，如果小堆比大堆多2，则将小堆里面的数据丢一个到大堆里面，最后如果两个堆长度一样，则一个堆吐出一个数据，平均值就是中位数；如果不一样，则小堆吐出来的就是结果。

面试推荐写第一个方法，毕竟简单，可以的话补充第二个思路

1
2
3
4
5
6
7
8
9
10
11
12
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
    total := make([]int, len(nums1)+len(nums2))
    copy(total, nums1)
    copy(total[len(nums1):], nums2)
    sort.Ints(total)
    
    if len(total)%2 == 0 {
        mid := len(total) >> 1
        return float64(total[mid-1]+total[mid]) / 2
    }
    return float64(total[len(total)>>1])
}

84. 柱状图中最大的矩形

image-20240607165306804

知识点：递增栈

使用递增栈，当出栈的时候，表示当前 idx 作为最高的时候，可以找到左边和右边。出栈的时候，左边是栈顶+1，右边是当前索引-1，高度是自身。

需要注意的是，最后还需要将栈里面的数据都拿出来，计算结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
func largestRectangleArea(heights []int) (res int) {
    // 单调递增栈，出来的时候 i 是右边，下一个栈是左边
    stack := make([]int, 0, len(heights))
    stack = append(stack, -1)
    
    for i, height := range heights {
        for len(stack) > 1 && heights[stack[len(stack)-1]] > height {
            // 出栈
            top := heights[stack[len(stack)-1]]
            stack = stack[:len(stack)-1]
            // 临时结果
            tmp := (i - stack[len(stack)-1]-1) * top
            //fmt.Println(top, i,tmp, res)
            if tmp > res {
                res = tmp
            }
        }
        stack = append(stack, i)
    }
    // fmt.Println(stack)
    // 剩余的出栈
    r := stack[len(stack)-1] + 1
    for len(stack) > 1 {
        // 出栈
        top := heights[stack[len(stack)-1]]
        stack = stack[:len(stack)-1]
        // 临时结果
        tmp := (r - stack[len(stack)-1] - 1) * top
        if tmp > res {
            res = tmp
        }
    }
    
    return res
}

295. 数据流的中位数

image-20240607171201137

知识点：堆

使用大堆和小堆，大堆，数据插入的时候往小堆插，小堆里面的数字往大堆移动。重点：为了确保大堆和小堆的大小符合条件，在移动的时候需要将大堆的数据往小堆回吐。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
type bHeap []int
type sHeap []int

func (b *bHeap) Len() int {
    return len(*b)
}

func (b *bHeap) Less(i, j int) bool {
    return (*b)[i] > (*b)[j]
}

func (b *bHeap) Swap(i, j int) {
    (*b)[i], (*b)[j] = (*b)[j], (*b)[i]
}

func (b *bHeap) Push(x interface{}) {
    (*b) = append((*b), x.(int))
}

func (b *bHeap) Pop() interface{} {
    x := (*b)[len(*b)-1]
    (*b) = (*b)[:len(*b)-1]
    return x
}

func (b *sHeap) Len() int {
    return len(*b)
}

func (b *sHeap) Less(i, j int) bool {
    return (*b)[i] < (*b)[j]
}

func (b *sHeap) Swap(i, j int) {
    (*b)[i], (*b)[j] = (*b)[j], (*b)[i]
}

func (b *sHeap) Push(x interface{}) {
    (*b) = append((*b), x.(int))
}

func (b *sHeap) Pop() interface{} {
    x := (*b)[len(*b)-1]
    (*b) = (*b)[:len(*b)-1]
    return x
}

type MedianFinder struct {
    bHeap bHeap
    sHeap sHeap
}

func Constructor() MedianFinder {
    return MedianFinder{
        bHeap: make([]int, 0, 100),
        sHeap: make([]int, 0, 100),
    }
}

func (this *MedianFinder) AddNum(num int) {
    heap.Push(&this.sHeap, num)
    if len(this.sHeap) == len(this.bHeap) {
        heap.Push(&this.sHeap, heap.Pop(&this.bHeap))
    }
    heap.Push(&this.bHeap, heap.Pop(&this.sHeap))
}

func (this *MedianFinder) FindMedian() float64 {
    // fmt.Println(this.bHeap)
    // fmt.Println(this.sHeap)
    if len(this.sHeap) != len(this.bHeap) {
        return float64(this.bHeap[0])
    } else {
        return float64(this.sHeap[0]+this.bHeap[0]) / 2.0
    }
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * obj := Constructor();
 * obj.AddNum(num);
 * param_2 := obj.FindMedian();
 */

32. 最长有效括号

image-20240612111121586

知识点：动态规划

局部问题到全局的扩展，使用动态规划。记录当结尾是 idx 时的最长子串长度。如果 s[idx] 是左括号，跳过，如果是右括号，则判断 s[len(s) - dp[idx-1]] 是否是左括号，如果是加上 dp[idx-1] 以及 左括号的左边。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
func longestValidParentheses(s string) (res int) {
    if len(s) == 0 {
        return 0
    }
    // 动态规划
    // 表示结尾是 i 时的最长有效括号
    dp := make([]int, len(s))
    // 初始化条件
    dp[0] = 0

    for i := 1; i < len(s); i++ {
        if s[i] == ')' {
            if i-dp[i-1]-1 >= 0 && s[i-dp[i-1]-1] == '(' {
                dp[i] = dp[i-1] + 2
                if i-dp[i-1]-2 >= 0 {
                    dp[i] += dp[i-dp[i-1]-2]
                }
            }
        }
        res = max(res, dp[i])
    }

    //fmt.Println(dp)

    return res
}